(*) GPUs are also very inefficient when it comes to synthesizing polygons which have a size lower than a few pixels, also called micropolygons. This is why minification scenarios should be avoided when rendering with GPU rasterizers : they generate aliased images at sub optimal speed. That's something I'll probably detail in another article :-).
Brief overview of tessellation in OpenGL4
OpenGL4 adds a new pipeline for geometry processing which is specifically intended for patch primitives. It has two additional programmable processing stages: the tessellation control stage and the tessellation evaluation stage.
Tessellation control stage
The tessellation control stage can be programmed using GLSL's tessellation control shading language, or replaced by calls to the glPatchParameter function. Its main goal is to provide subdivision levels to a tessellator (implemented in specific hardware in OpenGL4 GPUs) which performs the actual subdivision later in the pipeline. It is important to note that when using the programmable approach, the shader is executed for each vertex of the input patch (clearly for performance reasons, as this model allows to evaluate the data in parallel). This means that per patch varyings are evaluated several times, so heavy computations should be avoided or limited if possible (see the code of the shaders I present for an example).
Tessellation evaluation stage
The tessellation evaluation stage begins once the hardware tessellator has finished subdividing a patch, and has to be programmed using GLSL's tessellation evaluation shading language. This is the stage where the new vertices can be assigned their own attributes, using information provided by the tessellator and/or varyings from previous stages.
Curved PN triangles
The Curved PN triangle was first introduced in 2001 in a paper called "Curved PN Triangles". This primitive can be built from a regular triangle (composed of three vertices and their normals) to produce a richer description than triangle meshes, which combines a displacement field and a normal field. Displacement field
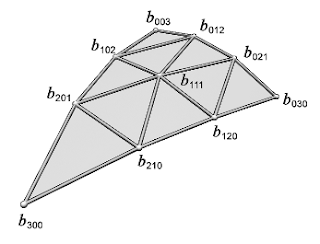
Let a triangle be defined by 3 vertices $V_i = (P_i, N_i)$, where $P_i$ is the position and $N_i$ the normalized normal of the ith vertex. The displacement field $b(u,v)$ of a PN Triangle is defined as follows: \[\begin{align}b(u,v)&=\sum_{i+j+k=3}b_{ijk}\frac{3!}{i!j!k!}u^i v^j w^k\\&=b_{300}w^3 + b_{030}u^3 + b_{003}v^3\\ &+ b_{210}3w^2u + b_{120}3wu^2 + b_{201}3w^2v \\ &+ b_{021}3u^2v + b_{102}3wv^2 + b_{012}3uv^2 \\ &+ b_{111}6wuv \end{align}\]
where $(u, v, w)$ are the barycentric coordinates relative to the vertices, and the terms $b_{ijk}$ are the control points of the PN Triangle. If we define $w_{ij} = (P_j - P_i) \cdot N_i $, then the control points verify:
Normal field
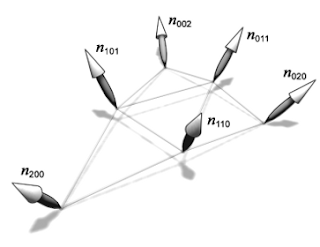
The normal field is described by a quadratic function $n(u,v)$ which is defined as:\[\begin{align} n(u,v) &=\sum_{i+j+k=2}n_{ijk}u^i v^j w^k \\ &= n_{200}w^2 + n_{020}u^2 + n_{002}v^2 \\ &+ n_{110}wu + n_{011}uv + n_{101}wv \end{align}\]
By defining $v_{ij} = 2 \frac{(P_j-P_i)\cdot(N_i + N_j)}{(P_j-P_i)\cdot(P_j-P_i)}$, we have:
| \[\begin{align} &n_{200}= N_1 \\ &n_{020}= N_2 \\ &n_{002}= N_3 \\ &n_{110}= \frac{N_1 + N_2 - v_{12}(P_2-P_1)}{\|N_1 + N_2 - v_{12}(P_2-P_1)\|} \\ &n_{011}= \frac{N_2 + N_3 - v_{23}(P_3-P_2)}{\|N_2 + N_3 - v_{23}(P_3-P_2)\|} \\ &n_{011}= \frac{N_3 + N_1 - v_{31}(P_1-P_3)}{\|N_3 + N_1 - v_{31}(P_1-P_3)\|}\end{align}\] |
|
|---|
GPU implementation
Now that we have the required equations to build the PN triangles, let's see how to implement this on the GPU. I'll just give the code of the two shaders and comment on what they're doing.Here's the the tessellation control shader code:
#version 420 core
// PN patch data
struct PnPatch
{
float b210;
float b120;
float b021;
float b012;
float b102;
float b201;
float b111;
float n110;
float n011;
float n101;
};
// tessellation levels
uniform float uTessLevels;
layout(vertices=3) out;
layout(location = 0) in vec3 iNormal[];
layout(location = 1) in vec2 iTexCoord[];
layout(location = 0) out vec3 oNormal[3];
layout(location = 3) out vec2 oTexCoord[3];
layout(location = 6) out PnPatch oPnPatch[3];
float wij(int i, int j)
{
return dot(gl_in[j].gl_Position.xyz - gl_in[i].gl_Position.xyz, iNormal[i]);
}
float vij(int i, int j)
{
vec3 Pj_minus_Pi = gl_in[j].gl_Position.xyz
- gl_in[i].gl_Position.xyz;
vec3 Ni_plus_Nj = iNormal[i]+iNormal[j];
return 2.0*dot(Pj_minus_Pi, Ni_plus_Nj)/dot(Pj_minus_Pi, Pj_minus_Pi);
}
void main()
{
// get data
gl_out[gl_InvocationID].gl_Position = gl_in[gl_InvocationID].gl_Position;
oNormal[gl_InvocationID] = iNormal[gl_InvocationID];
oTexCoord[gl_InvocationID] = iTexCoord[gl_InvocationID];
// set base
float P0 = gl_in[0].gl_Position[gl_InvocationID];
float P1 = gl_in[1].gl_Position[gl_InvocationID];
float P2 = gl_in[2].gl_Position[gl_InvocationID];
float N0 = iNormal[0][gl_InvocationID];
float N1 = iNormal[1][gl_InvocationID];
float N2 = iNormal[2][gl_InvocationID];
// compute control points
oPnPatch[gl_InvocationID].b210 = (2.0*P0 + P1 - wij(0,1)*N0)/3.0;
oPnPatch[gl_InvocationID].b120 = (2.0*P1 + P0 - wij(1,0)*N1)/3.0;
oPnPatch[gl_InvocationID].b021 = (2.0*P1 + P2 - wij(1,2)*N1)/3.0;
oPnPatch[gl_InvocationID].b012 = (2.0*P2 + P1 - wij(2,1)*N2)/3.0;
oPnPatch[gl_InvocationID].b102 = (2.0*P2 + P0 - wij(2,0)*N2)/3.0;
oPnPatch[gl_InvocationID].b201 = (2.0*P0 + P2 - wij(0,2)*N0)/3.0;
float E = ( oPnPatch[gl_InvocationID].b210
+ oPnPatch[gl_InvocationID].b120
+ oPnPatch[gl_InvocationID].b021
+ oPnPatch[gl_InvocationID].b012
+ oPnPatch[gl_InvocationID].b102
+ oPnPatch[gl_InvocationID].b201 ) / 6.0;
float V = (P0 + P1 + P2)/3.0;
oPnPatch[gl_InvocationID].b111 = E + (E - V)*0.5;
oPnPatch[gl_InvocationID].n110 = N0+N1-vij(0,1)*(P1-P0);
oPnPatch[gl_InvocationID].n011 = N1+N2-vij(1,2)*(P2-P1);
oPnPatch[gl_InvocationID].n101 = N2+N0-vij(2,0)*(P0-P2);
// set tess levels
gl_TessLevelOuter[gl_InvocationID] = uTessLevels;
gl_TessLevelInner[0] = uTessLevels;
}
The control points ($b_{ijk}$) and normal coefficients ($n_{ijk}$) are computed using the equations described in the previous section, and passed on to the next stage. Note that in order to avoid evaluating these attributes three times, I use the gl_InvocationID to compute a single component of the 3d vectors.
Now on to the tessellation evaluation:
#version 420 core
// PN patch data
struct PnPatch
{
float b210;
float b120;
float b021;
float b012;
float b102;
float b201;
float b111;
float n110;
float n011;
float n101;
};
uniform mat4 uModelViewProjection; // mvp
uniform float uTessAlpha; // controls the deformation
layout(triangles, fractional_odd_spacing, ccw) in;
layout(location = 0) in vec3 iNormal[];
layout(location = 3) in vec2 iTexCoord[];
layout(location = 6) in PnPatch iPnPatch[];
layout(location = 0) out vec3 oNormal;
layout(location = 1) out vec2 oTexCoord;
#define b300 gl_in[0].gl_Position.xyz
#define b030 gl_in[1].gl_Position.xyz
#define b003 gl_in[2].gl_Position.xyz
#define n200 iNormal[0]
#define n020 iNormal[1]
#define n002 iNormal[2]
#define uvw gl_TessCoord
void main()
{
vec3 uvwSquared = uvw*uvw;
vec3 uvwCubed = uvwSquared*uvw;
// extract control points
vec3 b210 = vec3(iPnPatch[0].b210, iPnPatch[1].b210, iPnPatch[2].b210);
vec3 b120 = vec3(iPnPatch[0].b120, iPnPatch[1].b120, iPnPatch[2].b120);
vec3 b021 = vec3(iPnPatch[0].b021, iPnPatch[1].b021, iPnPatch[2].b021);
vec3 b012 = vec3(iPnPatch[0].b012, iPnPatch[1].b012, iPnPatch[2].b012);
vec3 b102 = vec3(iPnPatch[0].b102, iPnPatch[1].b102, iPnPatch[2].b102);
vec3 b201 = vec3(iPnPatch[0].b201, iPnPatch[1].b201, iPnPatch[2].b201);
vec3 b111 = vec3(iPnPatch[0].b111, iPnPatch[1].b111, iPnPatch[2].b111);
// extract control normals
vec3 n110 = normalize(vec3(iPnPatch[0].n110,
iPnPatch[1].n110,
iPnPatch[2].n110));
vec3 n011 = normalize(vec3(iPnPatch[0].n011,
iPnPatch[1].n011,
iPnPatch[2].n011));
vec3 n101 = normalize(vec3(iPnPatch[0].n101,
iPnPatch[1].n101,
iPnPatch[2].n101));
// compute texcoords
oTexCoord = gl_TessCoord[2]*iTexCoord[0]
+ gl_TessCoord[0]*iTexCoord[1]
+ gl_TessCoord[1]*iTexCoord[2];
// normal
vec3 barNormal = gl_TessCoord[2]*iNormal[0]
+ gl_TessCoord[0]*iNormal[1]
+ gl_TessCoord[1]*iNormal[2];
vec3 pnNormal = n200*uvwSquared[2]
+ n020*uvwSquared[0]
+ n002*uvwSquared[1]
+ n110*uvw[2]*uvw[0]
+ n011*uvw[0]*uvw[1]
+ n101*uvw[2]*uvw[1];
oNormal = uTessAlpha*pnNormal + (1.0-uTessAlpha)*barNormal;
// compute interpolated pos
vec3 barPos = gl_TessCoord[2]*b300
+ gl_TessCoord[0]*b030
+ gl_TessCoord[1]*b003;
// save some computations
uvwSquared *= 3.0;
// compute PN position
vec3 pnPos = b300*uvwCubed[2]
+ b030*uvwCubed[0]
+ b003*uvwCubed[1]
+ b210*uvwSquared[2]*uvw[0]
+ b120*uvwSquared[0]*uvw[2]
+ b201*uvwSquared[2]*uvw[1]
+ b021*uvwSquared[0]*uvw[1]
+ b102*uvwSquared[1]*uvw[2]
+ b012*uvwSquared[1]*uvw[0]
+ b111*6.0*uvw[0]*uvw[1]*uvw[2];
// final position and normal
vec3 finalPos = (1.0-uTessAlpha)*barPos + uTessAlpha*pnPos;
gl_Position = uModelViewProjection * vec4(finalPos,1.0);
}
The tessellation control shader will compute the control points ($b_{ijk}$) and the normal components ($n_{ijk}$) of the PN Triangle, while the tessellation evaluation shader will compute the positions ($b(u,v)$) and normals ($n(u,v)$) of the final tessellated geometry. The barycentric coordinates are given by the built-in variable gl_TessCoord. The uTessAlpha variable is used to morph from a full PN Triangle tessellation (uTessAlpha = 1) to the planar tessellation (uTessAlpha = 0), you can tweak it in the demo.
Phong tessellation
Phong tessellation is an article which was published in 2008. It introduces a geometric version of Phong normal interpolation. The algorithm works with the same input as PN triangles (triangular patches, with positions and normals).
Model
The idea is to project each generated vertex on the tangent planes of the three vertices defining the patch it originates from, and then interpolate these projections using the barycentric coordinates (see figure 3).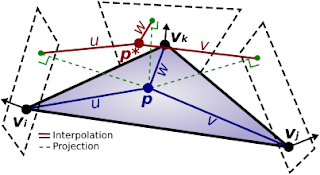 |
| Figure 3: Illustration of the Phong tessellation method. |
\[\begin{align} \mathbf{p}^{*}(u,v) &= u^{2}\mathbf{p}_i + v^{2}\mathbf{p}_{j}+ w^{2}\mathbf{p}_k + uv (\boldsymbol{\pi}_i(\mathbf{p}_j) + \boldsymbol{\pi}_j(\mathbf{p}_i)) \\&+ vw(\boldsymbol{\pi}_j(\mathbf{p}_k) + \boldsymbol{\pi}_k(\mathbf{p}_j)) + wu(\boldsymbol{\pi}_k(\mathbf{p}_i) + \boldsymbol{\pi}_i(\mathbf{p}_k)) \end{align}\]
GPU implementation
Implementing Phong tessellation is pretty straightforward if you've understood the PN triangle implentation. I'll just give the code, but won't comment it.Tessellation control:
#version 420 core
// Phong tess patch data
struct PhongPatch
{
float termIJ;
float termJK;
float termIK;
};
uniform float uTessLevels;
layout(vertices=3) out;
layout(location = 0) in vec3 iNormal[];
layout(location = 1) in vec2 iTexCoord[];
layout(location=0) out vec3 oNormal[3];
layout(location=3) out vec2 oTexCoord[3];
layout(location=6) out PhongPatch oPhongPatch[3];
#define Pi gl_in[0].gl_Position.xyz
#define Pj gl_in[1].gl_Position.xyz
#define Pk gl_in[2].gl_Position.xyz
float PIi(int i, vec3 q)
{
vec3 q_minus_p = q - gl_in[i].gl_Position.xyz;
return q[gl_InvocationID] - dot(q_minus_p, iNormal[i])
* iNormal[i][gl_InvocationID];
}
void main()
{
// get data
gl_out[gl_InvocationID].gl_Position = gl_in[gl_InvocationID].gl_Position;
oNormal[gl_InvocationID] = iNormal[gl_InvocationID];
oTexCoord[gl_InvocationID] = iTexCoord[gl_InvocationID];
// compute patch data
oPhongPatch[gl_InvocationID].termIJ = PIi(0,Pj) + PIi(1,Pi);
oPhongPatch[gl_InvocationID].termJK = PIi(1,Pk) + PIi(2,Pj);
oPhongPatch[gl_InvocationID].termIK = PIi(2,Pi) + PIi(0,Pk);
// tesselate
gl_TessLevelOuter[gl_InvocationID] = uTessLevels;
gl_TessLevelInner[0] = uTessLevels;
}
Tessellation evaluation:#version 420 core
// Phong tess patch data
struct PhongPatch
{
float termIJ;
float termJK;
float termIK;
};
uniform float uTessAlpha;
uniform mat4 uModelViewProjection;
layout(triangles, fractional_odd_spacing, ccw) in;
layout(location=0) in vec3 iNormal[];
layout(location=3) in vec2 iTexCoord[];
layout(location=6) in PhongPatch iPhongPatch[];
layout(location=0) out vec3 oNormal;
layout(location=1) out vec2 oTexCoord;
#define Pi gl_in[0].gl_Position.xyz
#define Pj gl_in[1].gl_Position.xyz
#define Pk gl_in[2].gl_Position.xyz
#define tc1 gl_TessCoord
void main()
{
// precompute squared tesscoords
vec3 tc2 = tc1*tc1;
// compute texcoord and normal
oTexCoord = gl_TessCoord[0]*iTexCoord[0]
+ gl_TessCoord[1]*iTexCoord[1]
+ gl_TessCoord[2]*iTexCoord[2];
oNormal = gl_TessCoord[0]*iNormal[0]
+ gl_TessCoord[1]*iNormal[1]
+ gl_TessCoord[2]*iNormal[2];
// interpolated position
vec3 barPos = gl_TessCoord[0]*Pi
+ gl_TessCoord[1]*Pj
+ gl_TessCoord[2]*Pk;
// build terms
vec3 termIJ = vec3(iPhongPatch[0].termIJ,
iPhongPatch[1].termIJ,
iPhongPatch[2].termIJ);
vec3 termJK = vec3(iPhongPatch[0].termJK,
iPhongPatch[1].termJK,
iPhongPatch[2].termJK);
vec3 termIK = vec3(iPhongPatch[0].termIK,
iPhongPatch[1].termIK,
iPhongPatch[2].termIK);
// phong tesselated pos
vec3 phongPos = tc2[0]*Pi
+ tc2[1]*Pj
+ tc2[2]*Pk
+ tc1[0]*tc1[1]*termIJ
+ tc1[1]*tc1[2]*termJK
+ tc1[2]*tc1[0]*termIK;
// final position
vec3 finalPos = (1.0-uTessAlpha)*barPos + uTessAlpha*phongPos;
gl_Position = uModelViewProjection * vec4(finalPos,1.0);
}
Note
The formulas and the variables in the shaders I introduce stick to the notations of the original articles.
Demo
Links / Valuable reads
- PN Triangles paper- Phong Tessellation paper
- GL_ATI_pn_triangles extension
Related articles:
- History of hardware tessellation
- 10 Fun things to do with tessellation
- First Contact with OpenGL 4.0 GPU Tessellation